2.2. Methods for correcting distortions

2.2.1. Introduction

For correcting radial and/or perspective distortion, we need to know a model to map between distorted space and undistorted space. Mapping from the undistorted space to the distorted space is the forward mapping (Fig. 5). The reverse process is the backward mapping or inverse mapping (Fig. 6).

Fig. 5 Forward mapping.

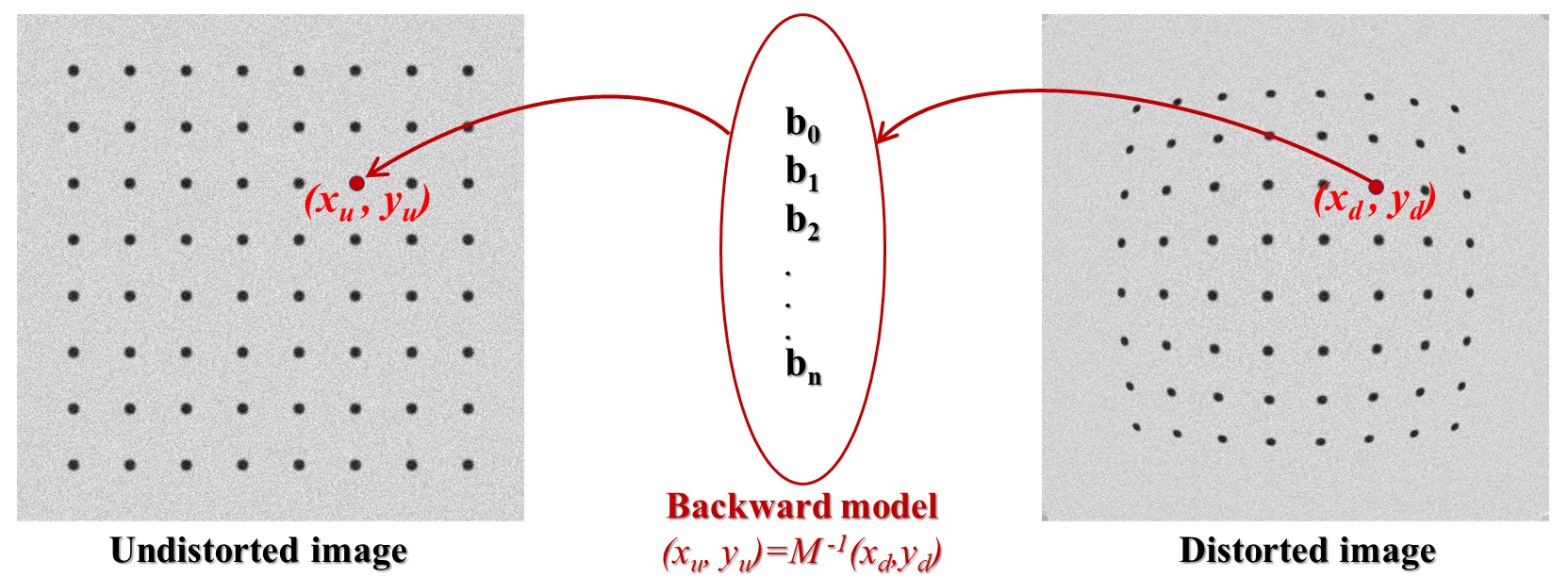
Fig. 6 Backward mapping.

There are many models which can be chosen from literature [R1, R2, R3] such as polynomial, logarithmic, field-of-view, or matrix-based models to describe the relationship between the undistorted space and distorted space. Some models were proposed for only one type of distortion while others are for both distortion types including the location of the optical center. From a selected model, we can find a practical approach to calculate the parameters of this model.

To calculate parameters of a distortion model, we have to determine the coordinates of reference points in the distorted space and their positions in the undistorted space, correspondingly. Reference points can be extracted using an image of a calibration object giving a line or dot-pattern image (Fig. 5), which is distorted. Using conditions that lines of these points must be straight, equidistant, parallel, or perpendicular we can estimate the locations of these reference-points in the undistorted space with high-accuracy.

Discorpy is the Python implementation of radial distortion correction methods presented in [C1]. These methods employ polynomial models and use a calibration image for calculating coefficients of the models where the optical center is determined independently. The reason of using these models and a calibration image is to achieve sub-pixel accuracy as strictly required by parallel-beam tomography systems. The methods were developed and used internally at the beamline I12, Diamond Light Source-UK, as Mathematica codes. In 2018, they were converted to Python codes and packaged as open-source software [R4] under the name Vounwarp. The name was changed to Discorpy in 2021. From version 1.4, methods for correcting perspective distortion [R3] and extracting reference points from a line-pattern image were added to the software. A key feature of methods developed and implemented in Discorpy is that radial distortion, center-of-distortion (optical center), and perspective distortion are determined independently using a single calibration image. The following sections explain methods implemented in Discorpy.

2.2.2. Extracting reference-points from a calibration image

The purpose of a calibration-image (Fig. 7 (a,b,c)) is to provide reference-points (Fig. 7 (d)) which can be extracted from the image using some image processing techniques. As shown in Fig. 7, there are a few calibration-images can be used in practice. A dot-pattern image (Fig. 7 (a)) is the easiest one to process because we just need to segment the dots and calculate the center-of-mass of each dot. For a line-pattern image (Fig. 7 (b)), a line-detection technique is needed. Points on the detected lines or the crossing points between these lines can be used as reference-points. For a chessboard image (Fig. 7 (c)), one can employ some corner-detection techniques or apply a gradient filter to the image and use a line-detection technique.

Fig. 7 (a) Dot-pattern image. (b) Line-pattern image. (c) Chessboard image. (d) Extracted reference-points from the image (a),(b), and (c).

In practice, acquired calibration images do not always look nice as shown in Fig. 7. Some are very challenging to get reference-points. The following sub-sections present practical approaches to process calibration images in such cases:

• 2.2.2.1. Pre-processing techniques for a dot-pattern image
• 2.2.2.2. Pre-processing techniques for a line-pattern image
• 2.2.2.3. Pre-processing techniques for a chessboard image

2.2.3. Grouping reference-points into horizontal lines and vertical lines

Different techniques of calculating parameters of a distortion-model use reference-points differently. The techniques [C1, R5] implemented in Discorpy group reference-points into horizontal lines and vertical lines (Fig. 15), represent them by the coefficients of parabolic fits, and use these coefficients for calculating distortion-parameters.

Fig. 15 (a) Points are grouped into horizontal lines. (b) Points are grouped into vertical lines.

The grouping step is critical in data processing workflow. It dictates the performance of other methods down the line. In Discorpy, the grouping method works by searching the neighbours of a point to decide if they belong to the same group or not. The search window is defined by the distance between two nearest reference-points, the slope of the grid, the parameter R, and the acceptable number of missing points. Depending on the quality of a calibration image, users may need to tweak parameters of pre-processing methods and/or the grouping method to get the best results (Fig. 16).

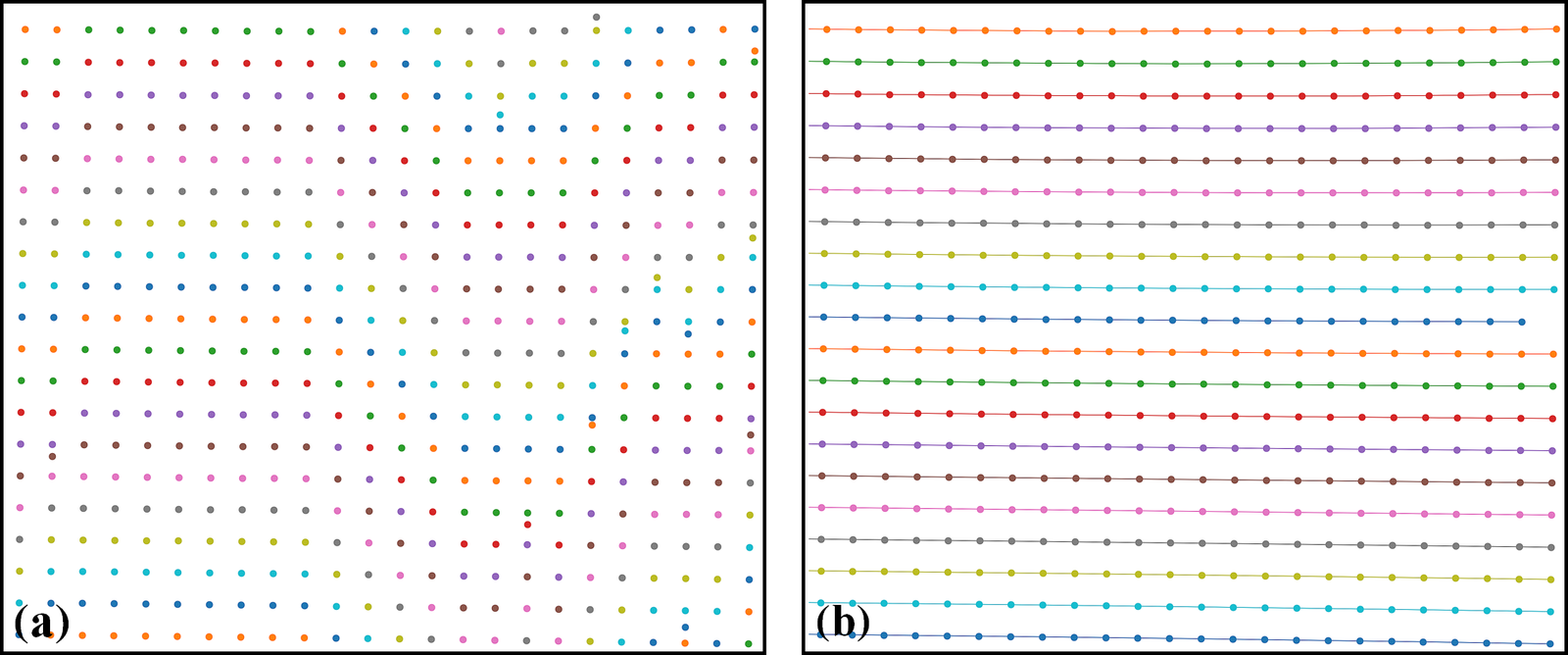
Fig. 16 (a) Points extracted from a calibration image including unwanted points. (b) Results of applying the grouping method to points in (a).

The coordinates of points on each group are fitted to parabolas in which horizontal lines are represented by

(1)\[y = {a_i}{x^2} + {b_i}{x} + {c_i}\]

and vertical lines by

(2)\[x = {a_j}{y^2} + {b_j}{y} + {c_j}\]

where \(i\), \(j\) are the index of the horizontal lines and vertical lines respectively.

2.2.4. Calculating the optical center of radial distortion

The coarse estimate of the center of distortion (COD) is explained in Fig. 17 where (\({x_0}\), \({y_0}\)) is the average of the axis intercepts \(c\) of two parabolas between which the coefficient \(a\) changes sign. The slopes of the red and green line are the average of the \(b\) coefficients of these parabolas.

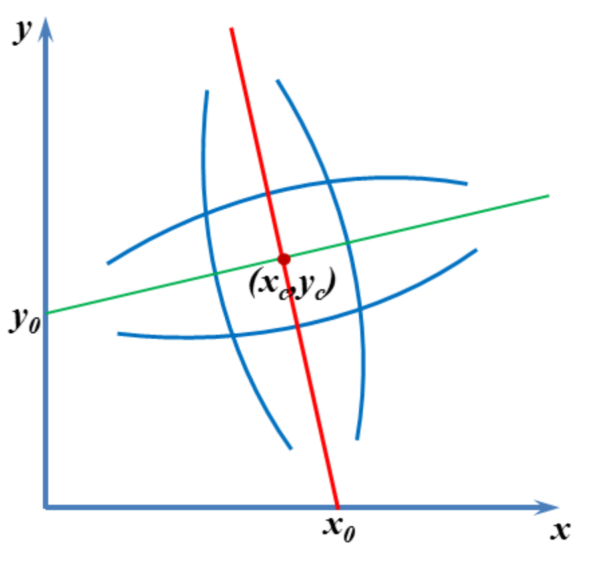
Fig. 17 Intersection between the red and the green line is the CoD.

For calculating the COD with high accuracy, Discorpy implements two methods. One approach is described in details in [R5] where the linear fit is applied to a list of (\(a\), \(c\)) coefficients in each direction to find x-center and y-center of the distortion. Another approach, which is slower but more accurate, is shown in [C1]. The technique varies the COD around the coarse-estimated COD and calculate a corresponding metric (Fig. 18). The best COD is the one having the minimum metric. This approach, however, is sensitive to perspective distortion. In practice, it is found that the coarse COD is accurate enough.

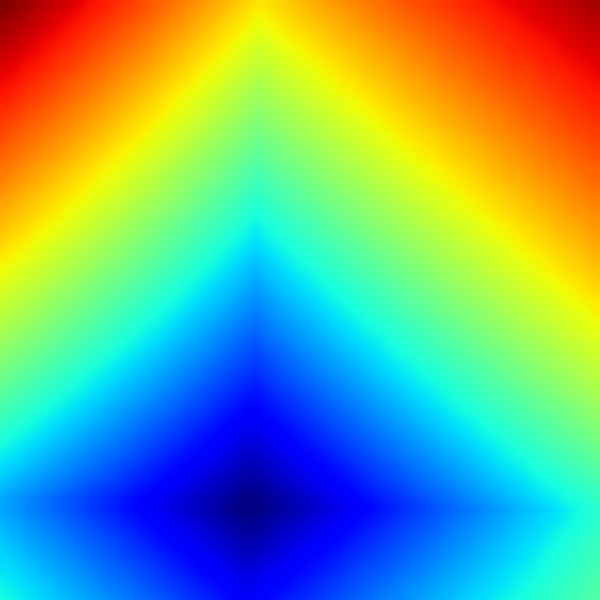
Fig. 18 Metric map of the CoD search.

2.2.5. Correcting perspective effect

In practice, a target sample may not be mounted in parallel to a sensor-plane, particularly for a high-resolution detector. This causes perspective distortion in the acquired image which affects the accuracy of a calculated model for radial distortion. Perspective distortion can be detected by making use of parabolic coefficients of lines [R5] where the origin of the coordinate system is shifted to the COD, calculated by the approach in [R5], before the parabola fitting. Fig. 19 (a) shows the plot of \(a\)-coefficients against \(c\)-coefficients for horizontal lines (Eq. (1)) and vertical lines (Eq. (2)). If there is perspective distortion, the slopes of straight lines fitted to the plotted data are different. The other consequence is that \(b\)-coefficients vary against \(c\)-coefficients instead of staying the same (Fig. 19 (b)). For comparison, corresponding plots of parabolic coefficients for the case of no perspective-distortion are shown in Fig. 20.

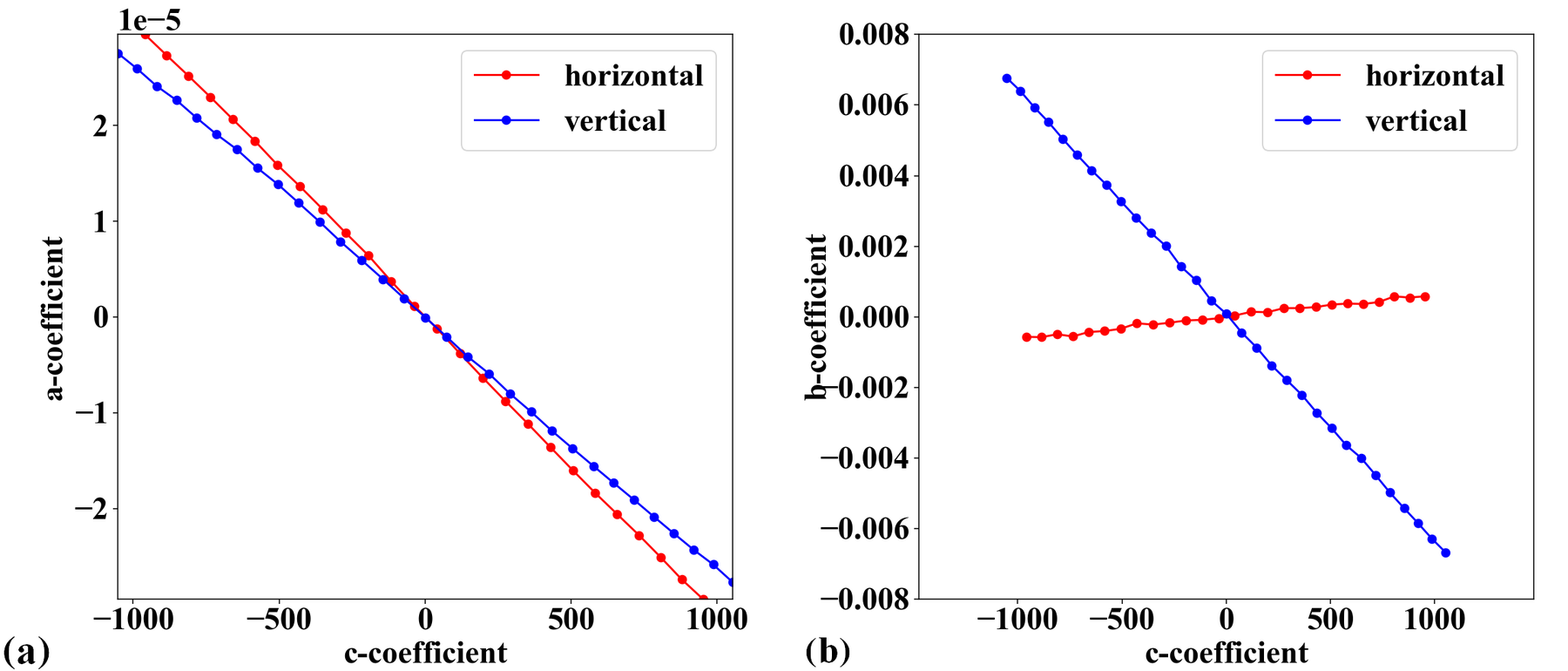
Fig. 19 Effects of perspective distortion to parabolic coefficients. (a) Between \(a\) and \(c\)-coefficients. (b) Between \(b\) and \(c\)-coefficients.

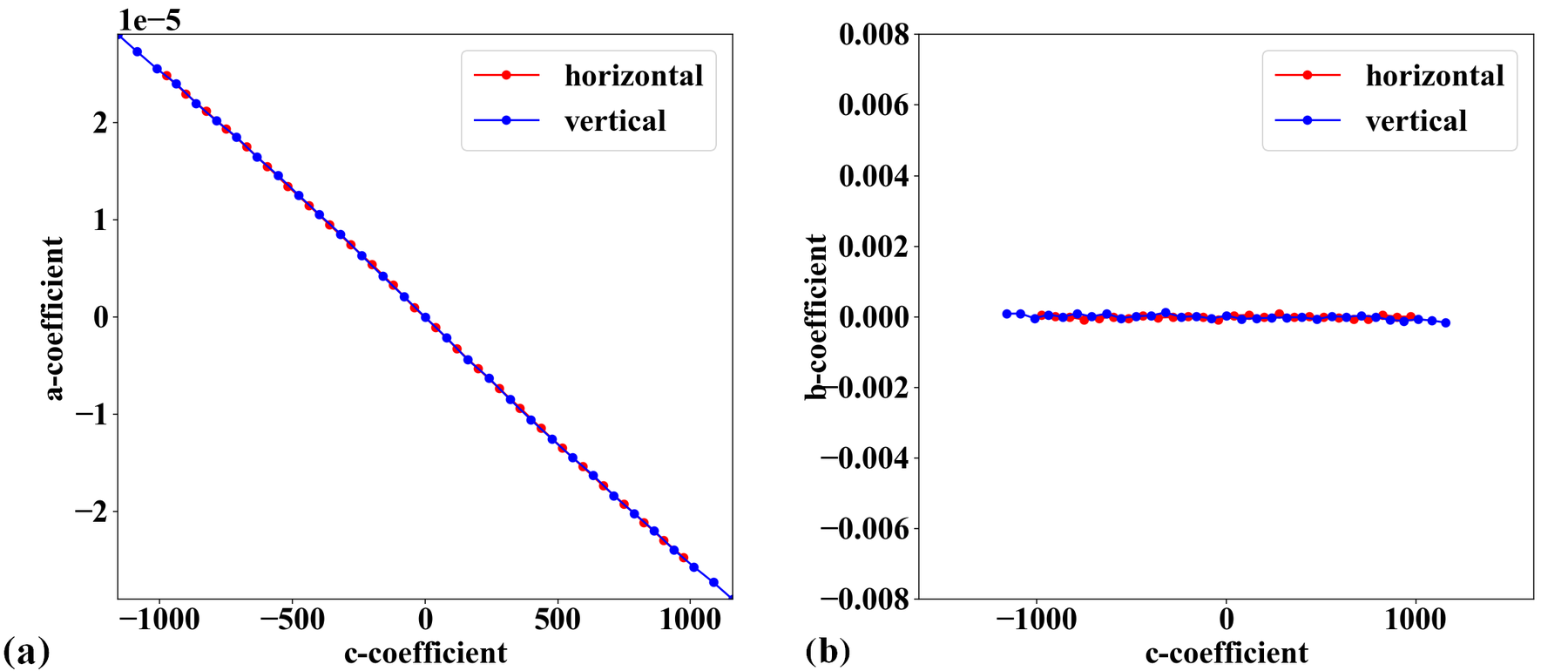
Fig. 20 (a) Corresponding to Fig. 19 (a) without perspective distortion. (b) Corresponding to Fig. 19 (b) without perspective distortion.

In Discorpy 1.4, a method for correcting perspective effect has been developed and added to the list of functionalities. This is a novel feature and has not yet been published in a journal. The method works by correcting coefficients of parabolas using the fact that the resulting coefficients have to satisfy the conditions as shown in Fig. 20. From the corrected coefficients, a grid of points are regenerated by finding cross points between parabolas. Details of the method can be found here.

2.2.6. Calculating coefficients of a polynomial model for radial-distortion correction

For sub-pixel accuracy, the models chosen in [C1] are as follows; for the forward mapping:

(3)\[\begin{align} \frac{r_u}{r_d} = \frac{x_u}{x_d} = \frac{y_u}{y_d} = k_0^f + {k_1^f}{r_d} + {k_2^f}{r_d^2} + {k_3^f}{r_d^3} + .. + {k_n^f}{r_d^n} \equiv F({r_d}) \end{align}\]

for the backward mapping:

(4)\[\begin{align} \frac{r_d}{r_u} = \frac{x_d}{x_u} = \frac{y_d}{y_u} = k_0^b + {k_1^b}{r_u} + {k_2^b}{r_u^2} + {k_3^b}{r_u^3} + .. + {k_n^b}{r_u^n} \equiv B({r_u}) \end{align}\]

\(({x_u}, {y_u})\) are the coordinate of a point in the undistorted space and \({r_u}\) is its distance from the COD. \(({x_d}, {y_d}, {r_d})\) are for a point in the distorted space. The subscript \(d\) is used for clarification. It can be omitted as in Eq. (1) and (2).

To calculate coefficients of two models, we need to determine the coordinates of reference-points in both the distorted-space and in the undistorted-space, correspondingly; and solve a system of linear equations. In [C1] this task is simplified by finding the intercepts of undistorted lines, \((c_i^u, c_j^u)\), instead. A system of linear equations for finding coefficients of the forward mapping is derived as

(5)\[\begin{split}\begin{align} \left( \begin{array}{ccccc} \vdots & \vdots & \ddots & \vdots & \vdots \\ 1 & r_d & {r_d^2} & \cdots & {r_d^n} \\ \vdots & \vdots & \ddots & \vdots\\ 1 & r_d & {r_d^2} & \cdots & {r_d^n} \\ \vdots & \vdots & \ddots & \vdots & \vdots \end{array} \right) \left(\begin{array}{c} k_0^f \\ k_1^f \\ k_2^f \\ \vdots \\ k_n^f \end{array} \right) = \left(\begin{array}{c} \vdots \\ {c_i^u}/({a_i}{x_d^2} + c_i) \\ \vdots \\ {c_j^u}/({a_j}{y_d^2} + c_j) \\ \vdots \end{array} \right) \end{align}\end{split}\]

where each reference-point provides two equations: one associated with a horizontal line (Eq. (1)) and one with a vertical line (Eq. (2)). For the backward mapping, the equation system is

(6)\[\begin{split}\begin{align} \left( \begin{array}{ccccc} \vdots & \vdots & \ddots & \vdots & \vdots \\ 1 & {r_d}/{F_i} & {r_d^2}/F_i^2 & \cdots & {r_d^n / F_i^n} \\ \vdots & \vdots & \ddots & \vdots\\ 1 & {r_d}/{F_j} & {r_d^2}/F_j^2 & \cdots & {r_d^n / F_j^n} \\ \vdots & \vdots & \ddots & \vdots & \vdots \end{array} \right) \left(\begin{array}{c} k_0^b \\ k_1^b \\ k_2^b \\ \vdots \\ k_n^b \end{array} \right) = \left(\begin{array}{c} \vdots \\ F_i \\ \vdots \\ F_j \\ \vdots \end{array} \right) \end{align}\end{split}\]

where \(F_i=({a_i}{x_d^2} + c_i)/c_i^u\) and \(F_j=({a_j}{y_d^2} + c_j)/c_j^u\). In practice, using distortion coefficients up to the fifth order is accurate enough, as there is no significant gain in accuracy with higher order. As can be seen, the number of linear equations, given by the number of reference-points, is much higher than the number of coefficients. This is crucial to achieve high accuracy in radial-distortion correction. Because the strength of distortion varies across an image, providing many reference-points with high-density improves the robustness of a calculated model.

To solve these above equations we need to determine \(c_i^u\) and \(c_j^u\). Using the assumption that lines are equidistant, \(c_i^u\) and \(c_j^u\) are calculated by extrapolating from a few lines around the COD as

(7)\[c_i^u=sgn(c_i) \times \vert (i - i_0) \overline{\Delta{c}} \vert + c_{i_0}\]

and

(8)\[c_j^u=sgn(c_j) \times \vert (j - j_0) \overline{\Delta{c}} \vert + c_{j_0}\]

where the \(sgn()\) function returns the value of -1, 0, or 1 corresponding to its input of negative, zero, or positive value. \(i_0\) is the index of the line closest to the COD. \(\overline{\Delta{c}}\) is the average of the difference of \(c_i\) near the COD. \(\overline{\Delta{c}}\) can be refined further by varying it around an initial guess and find the minimum of \(\sum_{i} (c_i - c_i^u)^2\) , which also is provided in the package.

Sometime we need to calculate coefficients of a backward model given that coefficients of the corresponding forward-model are known, or vice versa. This is straightforward as one can generate a list of reference-points and calculate their positions in the opposite space using the known model. From the data-points of two spaces and using Eq. (3) or Eq. (4) directly, a system of linear equations can be formulated and solved to find the coefficients of the opposite model. This functionality is available in Discorpy.

2.2.7. Calculating coefficients of a correction model for perspective distortion

The forward mapping between a distorted point and an undistorted point are given by [R3]

(9)\[x_u = \frac{{k_1^f}{x_d} + {k_2^f}{y_d} + k_3^f}{{k_7^f}{x_d} + {k_8^f}{y_d} + 1}\]

(10)\[y_u = \frac{{k_4^f}{x_d} + {k_5^f}{y_d} + k_6^f}{{k_7^f}{x_d} + {k_8^f}{y_d} + 1}\]

These equations can be rewritten as

(11)\[\begin{align} x_u = &{k_1^f}{x_d} + {k_2^f}{y_d} + k_3^f + 0 \times {k_4^f} + 0 \times {k_5^f} + 0 \times {k_6^f} - {k_7^f}{x_d}{x_u} - {k_8^f}{y_d}{x_u} \end{align}\]

(12)\[\begin{align} y_u = 0 \times {k_1^f} + 0 \times {k_2^f} + 0 \times {k_3^f} + {k_4^f}{x_d} + {k_5^f}{y_d} + k_6^f - {k_7^f}{x_d}{y_u} - {k_8^f}{y_d}{y_u} \end{align}\]

which can be formulated as a system of linear equations for n couple-of-points (1 distorted point and its corresponding point in the undistorted space).

(13)\[\begin{split}\begin{align} \left( \begin{array}{cccccccc} x_{d1} & y_{d1} & 1 & 0 & 0 & 0 & -x_{d1}x_{u1} & -y_{d1}x_{u1} \\ 0 & 0 & 0 & x_{d1} & y_{d1} & 1 & -x_{d1}y_{u1} & -y_{d1}y_{u1} \\ x_{d2} & y_{d2} & 1 & 0 & 0 & 0 & -x_{d2}x_{u2} & -y_{d2}x_{u2} \\ 0 & 0 & 0 & x_{d2} & y_{d2} & 1 & -x_{d2}y_{u2} & -y_{d2}y_{u2} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ x_{dn} & y_{dn} & 1 & 0 & 0 & 0 & -x_{dn}x_{un} & -y_{dn}x_{un} \\ 0 & 0 & 0 & x_{dn} & y_{dn} & 1 & -x_{dn}y_{un} & -y_{dn}y_{un} \end{array} \right) \left(\begin{array}{c} k_1^f \\ k_2^f \\ k_3^f \\ k_4^f \\ k_5^f \\ k_6^f \\ k_7^f \\ k_8^f \end{array} \right) = \left(\begin{array}{c} x_{u1} \\ y_{u1} \\ x_{u2} \\ y_{u2} \\ \vdots \\ x_{un} \\ y_{un} \end{array} \right) \end{align}\end{split}\]

For the backward mapping, the coordinates of corresponding points in Eq. (9-13) are simply swapped which results in

(14)\[x_d = \frac{{k_1^b}{x_u} + {k_2^b}{y_u} + k_3^b}{{k_7^b}{x_u} + {k_8^b}{y_u} + 1}\]

(15)\[y_d = \frac{{k_4^b}{x_u} + {k_5^b}{y_u} + k_6^b}{{k_7^b}{x_u} + {k_8^b}{y_u} + 1}\]

(16)\[\begin{split}\begin{align} \left( \begin{array}{cccccccc} x_{u1} & y_{u1} & 1 & 0 & 0 & 0 & -x_{u1}x_{d1} & -y_{u1}x_{d1} \\ 0 & 0 & 0 & x_{u1} & y_{u1} & 1 & -x_{u1}y_{d1} & -y_{u1}y_{d1} \\ x_{u2} & y_{u2} & 1 & 0 & 0 & 0 & -x_{u2}x_{d2} & -y_{u2}x_{d2} \\ 0 & 0 & 0 & x_{u2} & y_{u2} & 1 & -x_{u2}y_{d2} & -y_{u2}y_{d2} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ x_{un} & y_{un} & 1 & 0 & 0 & 0 & -x_{un}x_{dn} & -y_{un}x_{dn} \\ 0 & 0 & 0 & x_{un} & y_{un} & 1 & -x_{un}y_{dn} & -y_{un}y_{dn} \end{array} \right) \left(\begin{array}{c} k_1^b \\ k_2^b \\ k_3^b \\ k_4^b \\ k_5^b \\ k_6^b \\ k_7^b \\ k_8^b \end{array} \right) = \left(\begin{array}{c} x_{d1} \\ y_{d1} \\ x_{d2} \\ y_{d2} \\ \vdots \\ x_{dn} \\ y_{dn} \end{array} \right) \end{align}\end{split}\]

To find 8 coefficients in Eq. (13) or Eq. (16), the coordinates of at least 4 couple-of-points are needed where 1 couple-of-points provides 2 equations. If there are more than 4 couple-of-points, a least square method is used to solve the equation. Given the coordinates of distorted points on grid lines, using conditions that lines connecting these points must be parallel, equidistant, or perpendicular we can calculate the coordinates of undistorted points (Fig. 21) correspondingly. Details of this implementation can be found in Discorpy’s API.

Fig. 21 Demonstration of generating undistorted points from perspective points. (a) Calibration image. (b) Extracted reference-points. (c) Undistorted points generated by using the conditions that lines are parallel in each direction, perpendicular between direction, and equidistant. As the scale between the distorted space and undistorted space are unknown, the distance between lines in the undistorted space can be arbitrarily chosen. Here the mean of distances in the distorted space is used.

2.2.8. Correcting a distorted image

To correct distorted images, backward models are used because values of pixels adjacent to a mapped point are known (Fig. 22). This makes it easy to perform interpolation.

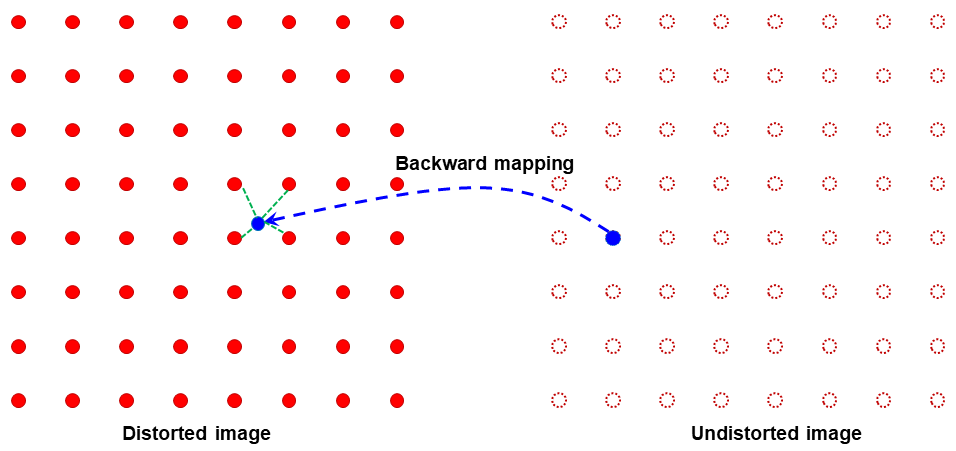
Fig. 22 Demonstration of the backward mapping.

For radial distortion; given \(({x_u}, {y_u})\) , \(({x_{COD}}, {y_{COD}})\), and \((k_0^b, k_1^b,..., k_n^b)\) of a backward model; the correction routine is as follows:

• -> Translate the coordinates: \(x_u = x_u - x_{COD}\); \(y_u = y_u - y_{COD}\).

• -> Calculate: \(r_u = \sqrt{x_u^2 + y_u^2}\); \(r_d = r_u(k_0^b + {k_1^b}{r_u} + {k_2^b}{r_u^2} + ... + {k_n^b}{r_u^n})\).

• -> Calculate: \(x_d = x_u{r_d / r_u}\); \(y_d = y_u{r_d / r_u}\).

• -> Translate the coordinates: \(x_d = x_d + x_{COD}\); \(y_d = y_d + y_{COD}\).

• -> Find 4 nearest grid points of the distorted image by combing two sets of [floor(\(x_d\)), ceil(\(x_d\))] and [floor(\(y_d\)), ceil(\(y_d\))]. Clip values out of the range of the grid.

• -> Interpolate the value at \(({x_d}, {y_d})\) using the values of 4 nearest points. Assign the result to the point \(({x_u}, {y_u})\) in the undistorted image.

Correcting perspective distortion is straightforward. Given \(({x_u}, {y_u})\) and coefficients \((k_1^b, k_2^b,..., k_8^b)\), Eq. (14) (15) are used to calculate \(x_d\), \(y_d\). Then, the image value at this location is calculated by interpolation as explained above.

2.2.9. Summary

The above sections present a complete workflow of calibrating a lens-coupled detector in a concise way. It can be divided into three stages: pre-processing stage is for extracting and grouping reference-points from a calibration image; processing stage is for calculating coefficients of correction models; and post-processing stage is for correcting images. Discorpy’s API is structured following this workflow including an input-output module.

As shown above, parameters of correction models for radial distortion and perspective distortion can be determined independently because reference-points in the undistorted space can be generated easily using methods available in Discorpy. Details of how to use Discorpy to process real data are shown in section 3.